Procedures

      Either using a spreadsheet program or paper, mark off a 40 x 40 grid to make the Transition Matrix. Mark the rows and columns 0 through 39. All of the numbers correspond to the spots on the board. 0 being GO through 39 being Boardwalk. The columns represent from what spot you are starting your roll from and the rows represent the probabilities of landing on any of the other spots. For example, the number on the grid corresponding with column 13, row 24 would be the number of if one started on spot 13 (States Ave.) the probability of landing on spot 24 (Illinois Ave.) To fill each of the spaces on the grid all factors must be accounted for. There are four factors.
      1. The Probability of the dice. Moving one spot has a probability of 0. Moving two or twelve spots have a probability of 1/36. Moving three or eleven spots have a probability of 1/18. Moving four or ten spots have a probability of 1/12. Moving five or nine spots have a probability of 1/9. Moving six or eight spots have a probability of 5/36. Finally, moving seven spots has a probability of 1/6. (See Dice Graph below)
      2. There are the Probabilities of the Chance and Community Chest cards. There are sixteen Community Chest cards. Fourteen of them don't move you anywhere, but one moves you to GO and the other moves you to JAIL. In this case you must take the probability that is in the Community Chest space that was just occupied and multiply it by 14/16. Then you would take that original probability of Community Chest space, multiply it by 1/16 and add that to spaces in rows 0 and 10 (GO and JAIL). For example lets say a space in row 2 (a chest space) has the probability of X on it. Then you would put in space 2 X*14/16 and in spaces 0 and 10 add X*1/16.
      There are also sixteen Chance cards. Six of them do not move you but ten of them do. They can move you to GO, JAIL, St. Charles Place, Nearest Utility, Illinois Ave., Boardwalk, Reading Railroad, Go back three spots, and two cards advance you to the nearest Railroad. These work just like Chest cards. For example lets say a space in row 7 (a chance space) as the probability of X on it. Then you would put in space 7 X*6/16 and in spaces mentioned add X*1/16. Also, in the case of the nearest Railroad add X*2/16.
      3. The GO TO JAIL spot. The spaces in row 30 (GO TO JAIL) are always equal to zero. Any probability received for that spot must be added to space 10. (JAIL)
      4. The triple doubles rule. If you get three doubles in secession you must go to JAIL. To compensate for this rule, all the values in the Transition Matrix must be multiplied by 215/216 except for all values in row 10 (JAIL), those numbers get 1/216 added to them. NOTE: This rule does not apply until the third "roll" (explained later). A player could never get triple doubles until the third "roll".
If you have Microsoft Excel 6.0 for Windows you can download a copy of the Transition Matrix.

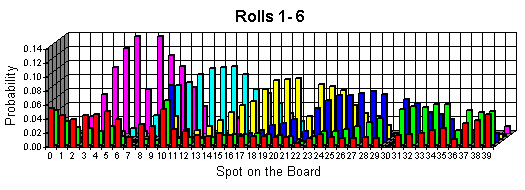
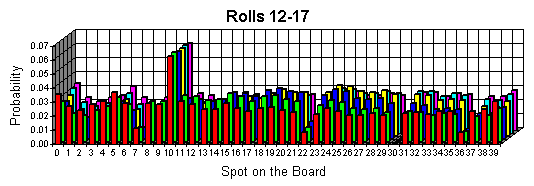
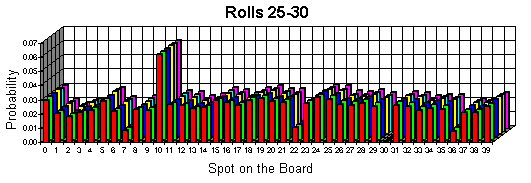
      After the Transition Matrix has been completed use a Graphics Calculator or a Matrix Algebra Program and put the information of the Transition Matrix into a 40 x 40 matrix and name it. In this case the matrix will be called A. Then, create a new 40 x 1 matrix with a 1 in the first space and zeros in all of the others, (because you always have a 100% chance of starting on GO), and call this 1. Then, multiply A * 1 to equal a new matrix 2. Then, multiply A * 2 to equal a new matrix 3. All the time recording the numbers in the new matrices. Each new matrix represents a "roll" (See Graphs of separate rolls below). Continue in this pattern until the numbers in the new matrices stabilize and remain the same, as seen in graphs of rolls 25-30. Those final numbers will be the probabilities the over all probabilities in the game.